In recent years, Assoc. Prof. Takata has become a frontrunner in knot theory research, attracting attention for the novel application of her research across genetics and other fields. While looking the part of a researcher who revels in finding regularity in numbers, she also enjoys relaxing to TV and anime. And with a reputation for being talkative, she is popular among students.
Assoc. Prof. Toshie Takata was born in the city of Yukuhashi in Fukuoka Prefecture. She first became interested in arithmetic at an early age, but it was in junior high that she developed her lifelong love of math, when she had a female mathematics teacher who encouraged her to think critically. Her high school mathematics teacher had earned his Ph.D. at Kyushu University and was the first person to suggest a career in research. In 1985, she entered the Department of Mathematics at the School of Science, Kyushu University. In 1990, despite high employability at the height of Japan’s economic bubble, she decided to go on to a master’s program after graduation, inspired by a topology program where an elder peer from independent study was studying. During the first year of her master’s program, her professor suggested she write her dissertation on the quantum invariants of knots, and she has been doing research ever since. "I owe everything to the people I’ve met along the way," she says. In 1993, she received a Ph.D. in Mathematical Sciences from the University of Tokyo. That same year, she returned to Kyushu University to work as a research associate in the Department of Mathematics in the Faculty of Science. After working as an associate professor at Niigata University from 2001 to 2009, she assumed her current position as associate professor at Kyushu University in 2010. She has published extensively as a leading expert in knot theory research, and with a passion for education, she enjoys giving guest lectures at high schools and holding mock lectures for prospective students during campus visits.
A: Trivial Knot | B: Trefoil Knot
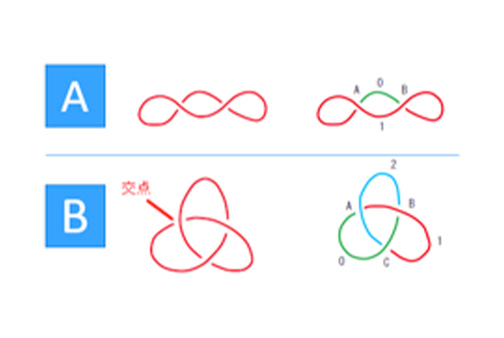
By coloring the knots, we can clearly see that they are not the same.
Assoc. Prof. Takata explains her research using a knot model. Strewn about the lab are stuffed animals still in their packaging. When asked why, she replies coyly, "I don't want to get them dirty..."
Diagraming knots is an essential part of preparing any research paper. A knot is proved by coloring each arc in a figure either red, blue, or green.
A: Trivial Knot | B: Trefoil Knot
By coloring the knots, we can clearly see that they are not the same.
First, let's talk about what knots are, their rules and definitions, and how we study them. Everyone knows that when you tie a string around a package, you try to tie it so that it won’t come loose. But in mathematics, knots are actually closed loops, where the two ends of a string are fused together. The simplest knot is one where the two ends of a string join to form a circle, which we call a trivial knot, or unknot. A rubber band is a perfect example of an unknot.
Assoc. Prof. Takata explains her research using a knot model. Strewn about the lab are stuffed animals still in their packaging. When asked why, she replies coyly, "I don't want to get them dirty..."
Knot theory, however, is the study of whether loops containing entanglements, or un-trivial knots, are the same or not. Take a look at Fig. 1. At first glance, A and B seem to be the same loop. In practice, however, loop A can be unwound while loop B cannot. And we can prove that A ≠ B by showing that the mathematical quantities computed for the knots take different values for A and B. As a side note, B is a knot known as the trefoil knot, named for its resemblance to a three-leaf clover.
Diagraming knots is an essential part of preparing any research paper. A knot is proved by coloring each arc in a figure either red, blue, or green.
A point where one piece intersects above or underneath another is called a crossing. In mathematics, the number of crossings can increase indefinitely, and the more crossings there are, the more complicated the knot becomes. Physical models can be made to predict simple knots like the one in the example above, but the more crossings there are, the more difficult it is to make such models. For such intricate knots, we use something known as a knot invariant. Because invariants have the same value for the same knot, if the values of the invariants for A and B are different, we can prove that A ≠ B. A well-known invariant is the Jones polynomial. Since its discovery, the theory of polynomial invariants of knots has developed significantly and has had a major impact on fields outside of math. There are currently more than 10,000 known knots with 14 classes of crossings, and we expect that the number of classes will only continue to grow. Finding powerful invariants that prove knot classification differences is a major research goal and dream of mine.
Although mathematics has been used in measurement and record-keeping for more than 2,000 years, knot theory is a relatively young field that only began in the 19th century. In recent years, expectations for the field have been on the rise in hopes applications will be found in various fields. Take genetics, for example. Since DNA is itself a kind of knot, knot theory may be able to determine whether two DNA structures are the same or not without the need for experimentation, and this could lead to predicting mutations, including those of intractable diseases. One familiar example is its application in graph theory when considering optimal configurations for subways, expressways, electrical circuits, and more. I conduct basic research, which means that it's done before considering real-world applications and, honestly, I don't know how it will be of use to society yet. But for me, I find joy in simply investigating knots and finding regularities in mathematical formulas. I think this kind of that innate human curiosity is what led to the development of mathematics in the first place and has also contributed to the growth and progress of society across all fields, including medicine and science.
In mathematics, no matter how difficult the problem, there is always an answer. Finding those answers is both the reward and the motivation for my research. The more elegant a solution or proof, the more beautiful—and the cooler—it is. And thought is all that is required for math. That’s another thing that makes math special: you can compete on the world stage using only your mind, regardless of gender or any other factor.
In the world of math, there are times when a sudden breakthrough leads to an increase in research materials and methods. Luckily for me, this happened when I started studying knot theory during the first year of my master’s program. At the time, we often made predictions based on a small amount of data obtained from calculating formulas by hand, but today it is much more common to make predictions and proofs using computers to generate the data from a large number of formulas. By plugging away at finding commonalities among huge sequences of generated numbers, we are able to find new solutions.
I can still remember the thrill I felt finding the answer to a geometry problem in elementary school just by drawing an auxiliary line! Put simply, my basic research lays the groundwork for the applied research that has an impact on the world. The world of mathematics is infinite, but it can be a challenge to create something from nothing. It's hard to express in words the sheer joy and sense of accomplishment you feel when you do.
The advantage of studying at Kyushu University is that there are so many choices to consider. More options means more possibilities. Mathematics is a wide-ranging discipline, but if during your studies you realize that it’s not for you, Kyushu University allows students to change trajectory and study other fields whenever they like.
Another big draw is the ability for students to discover the impact that pure mathematics and applied mathematics can have on society and in real life through the university’s internship scheme and its Institute of Mathematics for Industry, which has collaborations in the sciences and with industry. There are plenty of international students at Kyushu University, too, so students have opportunities to interact with the wider world around them.
Assoc. Prof. Takata brings a bento to the office every day. She loves bright colors like red, pink, and orange, so naturally, she is particular about her choice of bag.
Assoc. Prof. Takata says she likes to take care of her things. She has had her pink, flower-patterned pencil case for ten years, and it contains lots of colored pencils, which she uses to draw figures and check research papers. She mentions the cute Hello Kitty charm at the end of the pencil case zipper. "Actually, I've always been an ardent Hello Kitty fan, and I still have the shitajiki pencil board I used in elementary school," she laughs.
Two Windows desktop PCs sit on her desk, which she uses for both writing papers and drawing figures of knots using special software. "My eyes get tired looking at formulas all day," she says, glancing at two huge 40-inch displays that she has inherited from a recently retired teacher.
School is an important time for making and embracing mistakes, so be bold and maximize your potential!
Your time at university all comes down to thinking for yourself. In academics and research alike, whether you are right or wrong largely depends on where your head is at. To reach the right conclusions, you have to go through the process of thinking for yourself. Recently a lot of students seem to be waiting for instructions from their teachers. It also feels like so many of them tend to choose the shortest path to reach their goals. They seem to think they can comprehend an entire research paper by merely reading its abstract, altogether omitting the process of actually reading the paper to fully understand the research. But students can’t develop critical thinking or writing skills this way. They seem to underestimate themselves and stay within what they think are the limits of their abilities.
When you’re a student, it’s OK to fail! Detours and diversions all become part of your personal narrative. If you’re interested in something, take a chance, and act immediately. In a controlled environment like university, being bold dramatically expands your potential. Try to appreciate each and every person you meet. It is thanks to the many people I have met that I have come this far in my career. The few years you are in university are a brief and precious time in your life. Don’t waste them in low power mode. Be bold and take chances!
This interview was conducted in November 2019.
