Information security is one of the most critical issues of today, and Professor Yasuda has immersed himself in the research behind the encryption technology that protects our data. He has made a name for himself as a young cryptography expert by taking a bold, mathematics-based approach to his research and is a member of the government-led CRYPTREC (Cryptography Research and Evaluation Committees). The loving father of three girls, Professor Yasuda is also a family man.
Professor Yasuda was born in Osaka and grew up in neighboring Nara Prefecture. As an elementary school student, he was addicted to sports, soccer in particular. He was even scouted by a professional soccer team and selected to represent Nara Prefecture, all but assuring himself a career as an athlete. But in junior high, he discovered a new passion for mathematics. For Professor Yasuda, math never felt like work, and he found it so interesting that he decided to pursue the subject at university, attending the Department of Mathematics at Kyoto University. After graduating in 2002, he went on to receive his Ph.D. in Mathematical Science from the Graduate School of Mathematical Sciences at the University of Tokyo in 2007. That same year, he joined Fujitsu Laboratories as a researcher, where he conducted security-related research on encryption technologies and the use of privacy-protected information. Since leaving Fujitsu in March 2015, he has held his current position at Kyushu University. Professor Yasuda is also a member of CRYPTREC, the Cryptography Research and Evaluation Committees, which is organized by the National Institute of Information and Communications Technology (NICT) within the Ministry of Internal Affairs and Communications and the Information-Technology Promotion Agency (IPA) within the Ministry of Economy, Trade and Industry. A proactive contributor to the university curricula, Professor Yasuda has a far-reaching professional impact that goes beyond the field of mathematics.
Professor Yasuda thoughtfully explains that in mathematics, there are many ways to arrive at an answer. "What ultimately makes it so fascinating is the ability to find a straightforward solution."
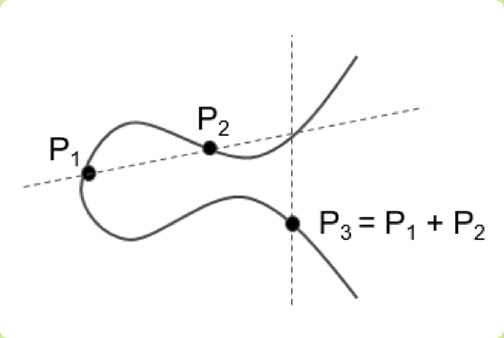An elliptical curve is defined by the equation y2 = x3 + ax + b, which is used in public-key cryptography. This simple yet effective equation is an example of strength in numbers, with values that can stretch into the hundreds or thousands of digits.
Research materials on one of Professor Yasuda's computers. When teaching, Professor Yasuda always includes images to make difficult concepts easier to understand. These images and illustrations come in handy during his high school visits, he explains: "I'm not teaching if students aren't learning."
Professor Yasuda thoughtfully explains that in mathematics, there are many ways to arrive at an answer. "What ultimately makes it so fascinating is the ability to find a straightforward solution."
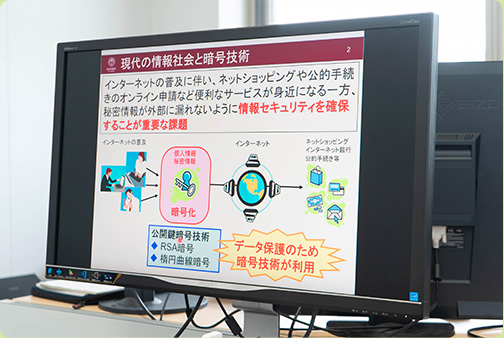
How do you use the internet? While we all enjoy the daily conveniences of online shopping and so many other online services, they come with the risk that our personal and confidential data could be leaked. As such, information security is one of the most important issues that we face in our modern internet society. For example, suppose you are booking a flight online. Your data is encrypted and sent to the service provider—in this case, the airline—where it is decrypted and used to process your request. Online encryption is what ensures that no one is eavesdropping on your data, often using one of two methods: RSA cryptography or elliptic-curve cryptography (ECC). Both are public-key cryptography systems that use two separate keys: one for encryption, which is made public, and one for decryption, which is kept secret.
An elliptical curve is defined by the equation y2 = x3 + ax + b, which is used in public-key cryptography. This simple yet effective equation is an example of strength in numbers, with values that can stretch into the hundreds or thousands of digits.
Different situations call for different encryptions. RSA cryptography is a secure form of encryption because of its long key size (or key length), but this uses a large amount of data, which slows down processing speeds. Credit card and online transactions are a familiar example of RSA encryption. Elliptic-curve cryptography, on the other hand, is lighter and faster than RSA cryptography. While RSA encryption is currently more widely used and can handle larger volumes of data, like the example of airline reservations, its key sizes are large at 2,048 bits, especially when compared to ECC keys, which require just 160 bits. My research focuses on ECC, which is commonly used for data protection in IC cards and student IDs, for copyright protection from piracy in Blu-Ray media, and to improve energy efficiency in electronic devices. ECC is also currently used in digital signatures of the cryptocurrency Bitcoin.
Research materials on one of Professor Yasuda's computers. When teaching, Professor Yasuda always includes images to make difficult concepts easier to understand. These images and illustrations come in handy during his high school visits, he explains: "I'm not teaching if students aren't learning."
Encryption technologies are derived from algorithms, which means that, in theory, they can be broken. Longer key lengths (larger amounts of data) require more time to crack, so theoretically the longer the key, the safer it is. But even the security of 1024-bit encryption, formerly a mainstream standard, was considered insufficient as of 2015. It is already estimated that 2048-bit encryption, the current recommended standard, will no longer be secure by 2030. While security has long been proportional to cost, with the advent of more advanced supercomputers, conventional encryption technologies may be cracked even earlier than expected. Competition is heating up around the globe as researchers race to develop next-generation encryption technologies like lattice-based cryptography.
With more and more research being published each day, cryptography has become one of the world's hottest industries. A recent conference in Japan drew close to 800 researchers. In 2010, a German university created a website where researchers from around the globe have continued to flock to compete in solving higher-order problems for next-generation encryption. For nearly ten years, everyone—my students and I included—has been trying to solve them. One of my students was even ranked 14th in the world at one point. As encryption continues to evolve, cryptography research, too, must try to keep up. And the more convenient the world becomes, the more secure data protection must be. So the question is, how can a mathematics-based approach to cryptography research help to integrate encryption into widely used services? Finding the answer to that question is my lifelong mission.
I love that I get to use mathematics for useful, real-world applications like encryption technology. My job is to make keys that are impossible to crack, which means that as I make them, I also have to learn how to break them. The field of cryptography is constantly flooded with dubious papers claiming to have developed some unbreakable cipher. There was once a paper that detailed a new and supposedly unbreakable type of encryption, to which I wrote an essay that refuted the claim and proved that this new encryption could, and would, be broken. [laughs] While there's always a definite answer to be found in mathematics, the subject itself is infinite. I'm always testing my decryption algorithms to find a key. It's a lot like my obsession with finding answers to math problems when I was a kid, which I think is why it's so interesting to me.
At the Institute of Mathematics for Industry, we link pure and applied mathematics with industry and science to help solve real-world mathematical challenges and develop much-needed technologies. Industry will often have a clear-cut problem that requires a technology for which the mathematical models don't exist yet. This means that the potential for research is infinite, and that's what makes this work so exciting—being able to create more opportunities for application.
I think Kyushu University provides an excellent environment for students to concentrate on their studies. Away from the city, students are free from distractions and information overload, which means they can focus on what matters to them and develop critical thinking skills. But at the same time, it's easy to become complacent here.
University is a time when attitude is everything, and Ito Campus allows students to explore different sides of themselves in a variety of settings across the humanities, social sciences, and natural sciences. The campus is also home to plenty of international students from around the world. I hope that students will make the most of their time here. It's not enough to specialize in a single field. Try to experience other fields of study and get to know other students and teachers. I genuinely think Kyushu University is an ideal place for students to experience real intellectual stimulation.
While Professor Yasuda used to be quite the athlete, he has had to stop playing sports due to a back injury. For long stints at the desk, he says that a seat cushion is indispensable to support his lower back and prevent the onset of pain.
Several computers and other devices are littered about Professor Yasuda's office, including some that are no longer used. One of them—a thin, lightweight laptop—has become an extension of his body, and he takes it with him wherever he goes. For computers and other electronics, he swears by Fujitsu, his former employer.
"Spiral notebooks lay flat, so it's easy to see both pages at once," Professor Yasuda explains, and has his secretary buy them in bulk. His notebooks are full of equations, all penned in thin handwriting. He is also particular about his pens and will only use red and black Zebra-brand Sarasa Clip 0.5mm pens.
Do your own thing! Put down your textbooks and look up at the world around you, starting right here in Kyushu.
There's a preconception that most people who study math at university end up becoming teachers. But I believe that mathematics can be useful in a much wider variety of contexts outside the classroom. I think you can do anything as long as you have a strong foundation in mathematics. I worked for a private corporation for seven and a half years and felt firsthand just how unforgiving the world can be. If a job doesn't work out, you can always try something new, but sometimes the change needs to come from within, or else the same issues will follow you wherever you go. What I'm trying to say is that you can't make a difference in the real world by merely studying math. I also want students to break free from the stereotype that math majors become math teachers. I would also add that I don't think that students should blindly believe everything their university professors say. Challenge everything. Think and act for yourself.
There are no certainties in university. The world is bigger than you think, and you won't expand your horizons by just studying at your desk. Participate in corporate internships and meet new people from other industries at business meet-ups—you just might come across something that interests you. Use your time at university to learn about what's going on in the world. It also helps to visualize where you want to be in five or ten years. Do this right, and you will be able to apply all that you have learned and experienced in the real world.
This interview was conducted in July 2019.
